ロボット
この章は、JJ. クレイグ著「ロボティクス ― 機構・力学・制御(Introduction to Robotics Mechanics and Control)」から、myCobotの利用に関するロボティクス用語を抜粋し、紹介しています。書籍の内容全体に興味有る方は、オンラインでお買い求めください。
1 背景
産業オートメーションの歴史はテクノロジーレベルの急速な革新によって形作られます。このようなオートメーション技術の革新は、世界経済の進歩を促す要素や結果と密接に関連するものです。1960年代の産業ロボットは間違いなくユニークなデバイスです。こうした産業ロボットはCAD/CAMシステム用途と組み合わせられています。これが現代の生産オートメーションの姿です。これらのテクノロジーが、産業オートメーションの新たな分野へ変化をリードしています。
マニピュレータは産業ロボットの中でも最も重要なタイプのロボットです。マニピュレータを産業ロボットと呼ぶのがふさわしいのかには議論があります。以下に挙げるロボットは、産業ロボットのカテゴリーに入っていると広く認識されているロボットですが、CNC(NC)グラインダーは普通は産業ロボットには含まれません。
ざっくりと言えば、マニピュレータのメカニズムの研究と操作の方法論は新たな分野の科学というわけではなく、従来の方法論を総合したものです。静的/動的環境でのマニピュレータの研究の方法論は工学を利用しています。マニピュレータの空間運動とその特徴を表すためには数学が使われています。様々な設計方法や、意図した動きや力を実現するためのアルゴリズムの評価には、操作論が利用されます。センサや産業ロボットのインターフェースデザインに利用されているのは電気工学のテクノロジーです。必要なタスクを動作させるプログラミングのプラットフォームにはコンピュータ技術が使われています。
2 ベースとなるコンセプト
ロボットアーム
ロボットアームは、産業ロボット、協働ロボット、マニピュレータアーム、バイオニックアーム、シリーズロボットなどとも呼ばれます。
位置と形状
ロボット研究においては、三次元的な空間の中での物体の位置を考えるのが一般的です。ここでいう物体とはマニピュレータのレバーやパーツ、グリッパーのことばかりではありません。マニピュレータが働く現場にあるその他の物体のことも指しています。こうした物体は二つの非常に重要な要素で表すことができます。「位置」と「形状」です。研究者たちは、一番はじめにこの二つのパラメータを数学的にどう表現し計算するべきかと考えます。
一般的に、空間的な物体の位置と形状を表すためには、参考となる枠を使用した空間座標システム内にその物体を設置することから始めます。その後、参考となる座標システム内のオブジェクトの位置と形状について考えます。
ダイレクトキネマティックス
キネマティックスとは、その動きを引き起こしている力を考慮しないで物体の動きを考えることです。キネマティックスにおいては、位置、速度、加速度、時間やその他の変数を考慮に入れた位置変数のうち、より上位のものについて考えます。つまり、マニピュレータキネマティックスであつかう物体とは、すべての動きの幾何学的で一時的な特徴だと言えます。ほとんどのマニピュレータはリジッドリンクで構成されています。リジッドリンクとは、動きを生み出すジョイントでつなぎ合わされた隣り合うリンク同士のことです。ジョイントが回転ジョイントなら、変移はジョイントアングルと呼ばれます。これらのジョイントは隣り合うバーの相対位置を測るポジションセンサと一緒に設置されているのが普通です。使用しているのが回転ジョイントなら、変移はジョイントアングルと呼ばれます。一部のマニピュレータにはスライド(もしくは可動)ジョイントがあり、隣り合う二つのリンクの変移はリニアに動きます。これはジョイントオフセットと呼ばれることもあります。
マニピュレータキネマティックスにおいて一般的に問題になるもののひとつが、マニピュレータフォワードキネマティックス(FK)です。マニピュレータに搭載されたエンドエフェクタの位置と形状を静的幾何学的に計算しようとするときに問題になります。特にジョイントアングルに値が設定されている場合、FKの問題は、ベースの座標システムに関連するツールの座標システムの位置と形状を計算することにあります。一般的には、このプロセスはジョイント空間座標からデカルト座標系に変換したマニピュレータの位置を表すことであると考えます。
自由度 ( DOF )
自由度の値とは、座標システム(参考となる枠)内のマニピュレータの位置の値に、マニピュレータ内の物体1-5を加えたものです。この座標システムは、機器を構成するすべての要素の位置を決定します。自由度はあらゆる機器に共通するものです。例えば4バー機構には3本の可動ロッドがありますが、自由度はひとつしかありません。標準的な産業ロボットでは、マニピュレータアームがほぼオープンなモーションチェーンであり、各ジョイントの位置が独自の値を持つため、ジョイントの数は自由度の数と等しくなっています。
エンドエフェクタ
エンドエフェクタは、マニピュレータの自由に動く末端に設置されています。ロボットの用途によっては、エンドエフェクタは機器を取り付けるパーツであったり、はんだごてであったり、電磁器などであったりします。マニピュレータの位置は、エンドエフェクタに取り付けられているツールの座標システムを利用して表されるのが一般的です。対応するツールの座標システムは、マニピュレータの固定ベースシステムに接続されているベースの座標システムです。
インバースキネマティックス(IK)
マニピュレータのエンドエフェクタの位置と形状を取得したら、取得した位置と形状に関するすべてのジョイントアングルを計算します。
3 空間の表し方
位置
座標システムを構築したら、3 x 1の位置ベクトルを使用して座標システム内のあらゆる点を回転することができます。多くの座標は座標システムで表されることが多いため、そのデータがどの座標システムで表されたものかを示す位置ベクトルを添付しておくことが重要です。本書で扱う位置ベクトルには、どの座標システムで表されたものかを示す注釈をつけています。
形状
空間内の点を示す以外にも、空間内の物体の形状を表すことも必要である場合が多くあります。例えば図2-2中のベクトルPは、マニピュレータハンドの指の間にある点を直接表し、ハンドの位置はその形状が分からない限り完全には決定できません。マニピュレータに充分な数のジョイントがあると仮定すれば、マニピュレータはどんな位置にあってもよく、指の間の点にも変位はありません。物体の形状を表すためには、物体上の座標システムを固定し、参考となる枠を考慮して、その座標システムの値を取得します。図2-2では、座標システムBは物体に何らかの方法で固定されていることが分かっています。Aと関連するBの値は、物体Aの形状を表すのに充分です。
座標システム
参考となる枠は、ある座標システムと他の座標システムとの関係を用いて表すことができます。参考となる枠には位置と形状の概念が含まれており、多くの場合、これら二つの概念の組み合わせであると考えることができます。位置は、回転マトリクスが単位行列であり、枠内の位置ベクトルがその点の位置を表すような枠で表されます。同様に、枠内の位置ベクトルがゼロベクトルである場合には、形状を表します。
4 DH パラメータ
定義
0=0.0に設定されている回転ジョイントnの場合、X軸の方向はX、軸と等しく、座標システムの原点(n)はd.=0.0を満たす点を選びます。プリズムジョイントnの場合には、軸8の方向は0.=0.0を満たすように設定されます。d.=0.0である場合、座標システムの原点(n)は、軸XN-1とジョイント軸nの交差する点を選びます。
リンク調整システムでは、リンク調整システムが上のようなリンクに固定されている場合、リンクのパラメータは以下のように表されます。
- α_i-1 :along x_i-1 : z_i-1とz_iの距離から動く
- アルファ_i-1 :aroundx_i-1 : z_i-1とz_iの角から回転する
- β_i :along z_i : x_i-1とx_iの距離から動く
- θ_i :aroundz_i :x_i-1とx_iの角から回転する
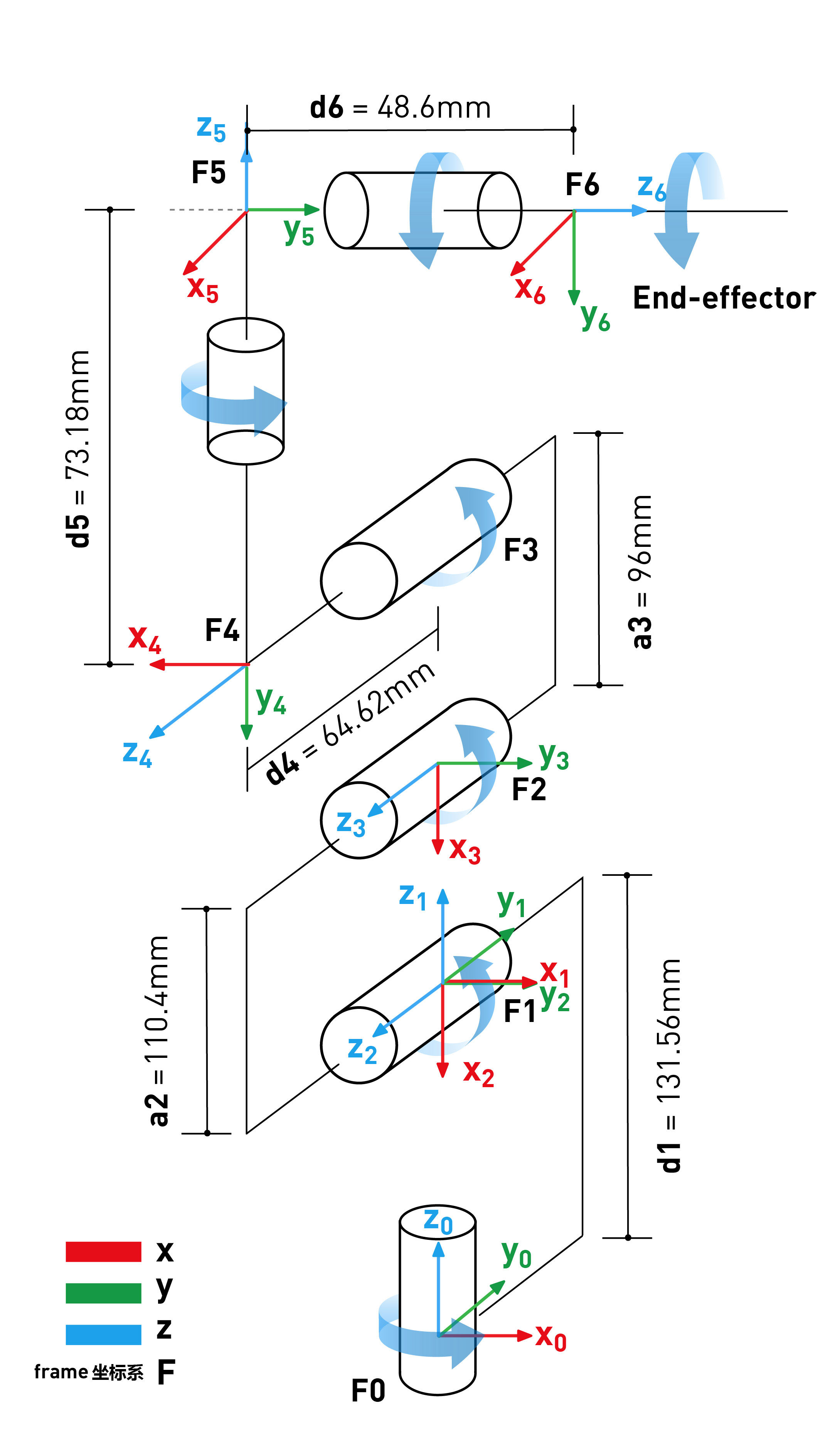
myCobotのDHパラメータ
| ジョイント | アルファ | α | β | θ | オフセット |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 131.56 | θ_1 | 0 |
| 2 | PI/2 | 0 | 0 | θ_2 | -PI/2 |
| 3 | 0 | -110.4 | 0 | θ_3 | 0 |
| 4 | 0 | -96 | 64.62 | θ_4 | -PI/2 |
| 5 | PI/2 | 0 | 73.18 | θ_5 | PI/2 |
| 6 | -PI/2 | 0 | 48.6 | θ_6 | 0 |
出典 : Elephant Robotics資料 Robot
